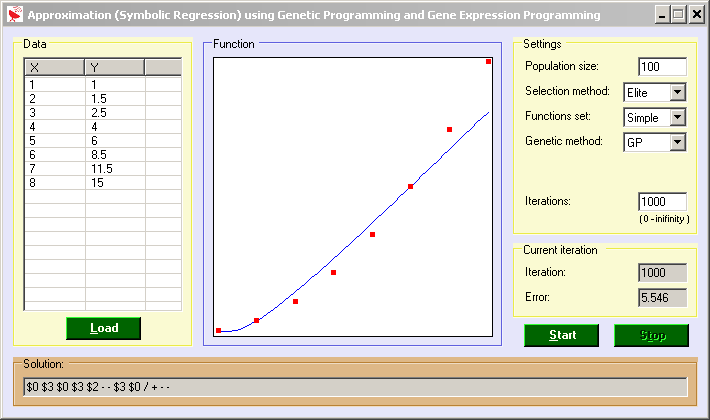
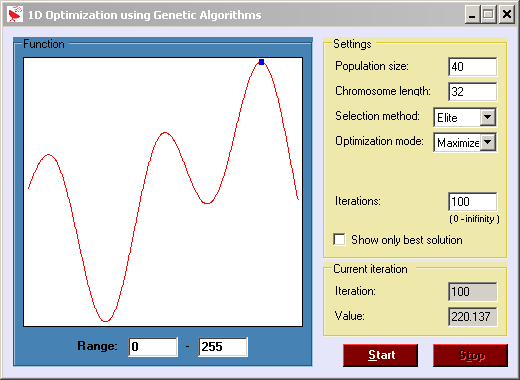
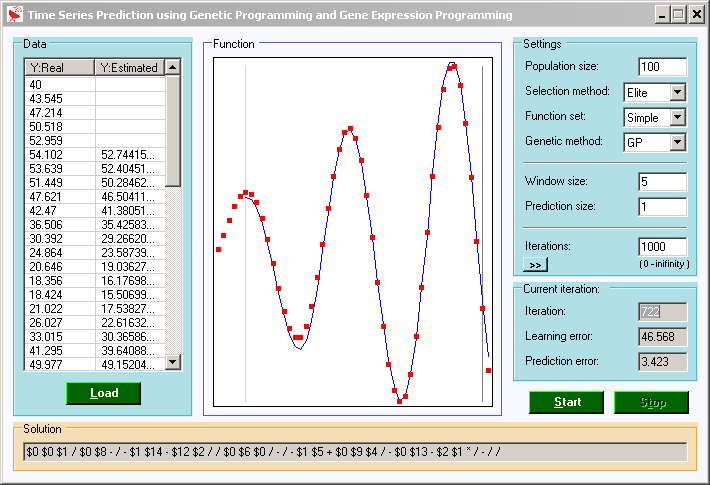
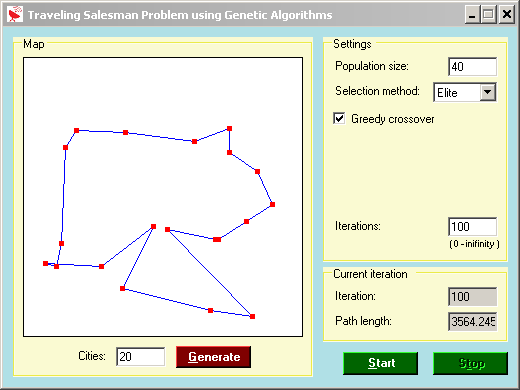
Genetic Approximation
A genetic algorithm (GA) is a search heuristic that mimics the process of
natural evolution. This heuristic is routinely used to generate useful solutions
to optimization and search problems. Genetic algorithms belong to the larger class
of evolutionary algorithms (EA), which generate solutions to optimization problems
using techniques inspired by natural evolution, such as inheritance, mutation, selection,
and crossover.
In a genetic algorithm, a population of strings (called chromosomes or the genotype
of the genome), which encode candidate solutions (called individuals, creatures,
or phenotypes) to an optimization problem, evolves toward better solutions. Traditionally,
solutions are represented in binary as strings of 0s and 1s, but other encodings
are also possible. The evolution usually starts from a population of randomly generated
individuals and happens in generations. In each generation, the fitness of every
individual in the population is evaluated, multiple individuals are stochastically
selected from the current population (based on their fitness), and modified (recombined
and possibly randomly mutated) to form a new population. The new population is then
used in the next iteration of the algorithm. Commonly, the algorithm terminates
when either a maximum number of generations has been produced, or a satisfactory
fitness level has been reached for the population. If the algorithm has terminated
due to a maximum number of generations, a satisfactory solution may or may not have
been reached.
Genetic algorithms find application in bioinformatics, phylogenetics, computational
science, engineering, economics, chemistry, manufacturing, mathematics, physics
and other fields.
A typical genetic algorithm requires:
- A genetic representation of the solution domain
- A fitness function to evaluate the solution domain
A standard representation of the solution is as an array of bits. Arrays of other
types and structures can be used in essentially the same way. The main property
that makes these genetic representations convenient is that their parts are easily
aligned due to their fixed size, which facilitates simple crossover operations.
Variable length representations may also be used, but crossover implementation is
more complex in this case. Tree-like representations are explored in genetic programming
and graph-form representations are explored in evolutionary programming.
The fitness function is defined over the genetic representation and measures the
quality of the represented solution. The fitness function is always problem dependent.
For instance, in the knapsack problem one wants to maximize the total value of objects
that can be put in a knapsack of some fixed capacity. A representation of a solution
might be an array of bits, where each bit represents a different object, and the
value of the bit (0 or 1) represents whether or not the object is in the knapsack.
Not every such representation is valid, as the size of objects may exceed the capacity
of the knapsack. The fitness of the solution is the sum of values of all objects
in the knapsack if the representation is valid, or 0 otherwise. In some problems,
it is hard or even impossible to define the fitness expression; in these cases,
interactive genetic algorithms are used.
Once we have the genetic representation and the fitness function defined, GA proceeds
to initialize a population of solutions randomly, then improve it through repetitive
application of mutation, crossover, inversion and selection operators.