|
Given the head of a linked list, find if it contains a loop or not, in linear time.
Can you accomplish it with only O(1) extra space? Can you do it without modifying
the list in any way?
|
- Hash Table: Traverse the list and store the pointers in a hash table. As soon as
you discover a collision, you’ve discovered a loop!
- List Reversal: Traverse the list and start reversing it. If there is a loop, you
shall revisit the head again. However, the “loop” in the list has been reversed
— to fix that, traverse the list again, reversing the pointers! When I posted the
following solution to a newsgroup many years ago, somebody pointed out that it is
a haiku :) “Start reversing the list. If you hit the head, there’s a loop”.
- Pointer Marking: In practice, linked lists are implemented using C structs with
at least a pointer; such a struct in C shall be 4-byte aligned. So the least significant
two bits are zeros. While traversing the list, you may ‘mark’ a pointer as traversed
by flipping the least significant bit. A second traversal is for clearing these
bits.
- Two Pointers: Start with two pointers pointing to the head. At each step, the ‘slower’
pointer moves forward only one step and the ‘faster’ pointer moves forward two steps.
If the faster pointer overtakes the slower pointer at any point of time, we have
discovered a loop! For more algorithmic ideas, check out Wikipedia article on Cycle
Detection.
boolean CheckIsItCircular(Node *list) {
Node * list1 = list;
Node * list2 = list;
while(list2) {
list1 = list1 -> next;
list2 = list2 -> next;
if(list2) list2 = list2 -> next;
else return false;
(list1 == list2) ) return true;
}
return false;
}
|
|
Write a Count() function that counts the number of times a given int occurs in a
list.
|
int Count(struct node* head, int searchFor) {
struct node* current = head;
int count = 0;
while (current != NULL) {
if (current->data == searchFor) count++;
current = current->next;
}
return count;
}
|
Write a GetNth() function that takes a linked list and an integer index and returns
the data value stored in the node at that index position. GetNth() uses the C numbering
convention that the first node is index 0, the second is index 1, ... and so on.
So for the list {42, 13, 666} GetNth() with index 1 should return 13. The index
should be in the range [0..length- 1]. If it is not, GetNth() should assert() fail
(or you could implement some other error case strategy).
|
Combine standard list iteration with the additional problem of counting over to
find the right node. Off-by-one errors are common in this sort of code. Check it
carefully against a simple case. If it's right for n=0, n=1, and n=2, it will probably
be right for n=1000.
int GetNth(struct node* head, int index) {
struct node* current = head;
int count = 0; // the index of the node we're currently looking at
while (current != NULL) {
if (count == index) return(current->data);
count++;
current = current->next;
}
assert(0); // if we get to this line, the caller was asking
// for a non-existent element so we assert fail.
}
|
|
You are given a pointer to a node (not the tail node) in a singly linked list. Delete
that node from the linked list. Write code in C.
|
void DeleteList(struct node** headRef) {
struct node* current = *headRef; // deref headRef to get the real head
struct node* next;
while (current != NULL) {
next = current->next; // note the next pointer
free(current); // delete the node
current = next; // advance to the next node
}
*headRef = NULL; // Again, deref headRef to affect the real head back
// in the caller.
}
|
|
Write a Pop() function that is the inverse of Push(). Pop() takes a non-empty list,
deletes the head node, and returns the head node's data. If all you ever used were
Push() and Pop(), then our linked list would really look like a stack. However,
we provide more general functions like GetNth() which what make our linked list
more than just a stack. Pop() should assert() fail if there is not a node to pop.
Here's some sample code which calls Pop()....
|
Extract the data from the head node, delete the node, advance the head pointer to
point at the next node in line. Uses a reference parameter since it changes the
head pointer.
int Pop(struct node** headRef) {
struct node* head = *headRef;
int result;
assert(head != NULL);
result = head->data; // pull out the data before the node is deleted
*headRef = head->next; // unlink the head node for the caller
// Note the * -- uses a reference-pointer
// just like Push() and DeleteList().
free(head); // free the head node
return(result); // don't forget to return the data from the link
}
|
|
A more difficult problem is to write a function InsertNth() which can insert a new
node at any index within a list. Push() is similar, but can only insert a node at
the head end of the list (index 0). The caller may specify any index in the range
[0..length], and the new node should be inserted so as to be at that index.
|
A more difficult problem is to write a function InsertNth() which can insert a new
node at any index within a list. Push() is similar, but can only insert a node at
the head end of the list (index 0). The caller may specify any index in the range
[0..length], and the new node should be inserted so as to be at that index.
This code handles inserting at the very front as a special case. Otherwise, it works
by running a current pointer to the node before where the new node should go. Uses
a for loop to march the pointer forward. The exact bounds of the loop (the use of
< vs <=, n vs. n-1) are always tricky — the best approach is to get the general
structure of the iteration correct first, and then make a careful drawing of a couple
test cases to adjust the n vs. n-1 cases to be correct. (The so called "OBOB" —
Off By One Boundary cases.) The OBOB cases are always tricky and not that interesting.
Write the correct basic structure and then use a test case to get the OBOB cases
correct. Once the insertion point has been determined, this solution uses Push()
to do the link in. Alternately, the 3-Step Link In code could be pasted here directly.
void InsertNthTest() {
struct node* head = NULL; // start with the empty list
InsertNth(&head, 0, 13); // build {13)
InsertNth(&head, 1, 42); // build {13, 42}
InsertNth(&head, 1, 5); // build {13, 5, 42}
DeleteList(&head); // clean up after ourselves
}
InsertNth() is complex — you will want to make some drawings to think about your
solution and afterwards, to check its correctness.
/*
A more general version of Push().
Given a list, an index 'n' in the range 0..length,
and a data element, add a new node to the list so
that it has the given index.
*/
void InsertNth(struct node** headRef, int index, int data) {
// position 0 is a special case...
if (index == 0) Push(headRef, data);
else {
struct node* current = *headRef;
int i;
for (i = 0; i < index -1; i++) {
ASSERT(current != NULL); // if this fails, index was too big
current = current->next;
}
assert(current != NULL); // tricky: you have to check one last time
Push(&(current->next), data); // Tricky use of Push() --
// The pointer being pushed on is not
// in the stack. But actually this works
// fine -- Push() works for any node pointer.
}
}
|
|
Write a SortedInsert() function which given a list that is sorted in increasing
order, and a single node, inserts the node into the correct sorted position in the
list. While Push() allocates a new node to add to the list, SortedInsert() takes
an existing node, and just rearranges pointers to insert it into the list. There
are many possible solutions to this problem.
|
The basic strategy is to iterate down the list looking for the place to insert the
new node. That could be the end of the list, or a point just before a node which
is larger than the new node. The three solutions presented handle the "head end"
case in different ways...
// Uses special case code for the head end
void SortedInsert(struct node** headRef, struct node* newNode)
{
// Special case for the head end
if (*headRef == NULL || (*headRef)->data >= newNode->data) {
newNode->next = *headRef;
*headRef = newNode;
}
else {
// Locate the node before the point of insertion
struct node* current = *headRef;
while (current->next != NULL && current->next->data < newnode->data) {
current = current->next;
}
newNode->next = current->next;
current->next = newNode;
}
}
// Dummy node strategy for the head end
void SortedInsert2(struct node** headRef, struct node* newNode)
{
struct node dummy;
struct node* current = &dummy;
dummy.next = *headRef;
while (current->next!=NULL && current->next->data < newNode->data) {
current = current->next;
}
newNode->next = current->next;
current->next = newNode;
*headRef = dummy.next;
}
// Local references strategy for the head end
void SortedInsert3(struct node** headRef, struct node* newNode)
{
struct node** currentRef = headRef;
while (*currentRef!=NULL && (*currentRef)->data < newNode->data) {
currentRef = &((*currentRef)->next);
}
newNode->next = *currentRef; // Bug: this line used to have
// an incorrect (*currRef)->next
*currentRef = newNode;
}
|
|
Write an InsertSort() function which given a list, rearranges its nodes so they
are sorted in increasing order. It should use SortedInsert().
|
Start with an empty result list. Iterate through the source list and SortedInsert()
each of its nodes into the result list. Be careful to note the .next field in each
node before moving it into the result list.
// Given a list, change it to be in sorted order (using SortedInsert()).
void InsertSort(struct node** headRef)
{
struct node* result = NULL; // build the answer here
struct node* current = *headRef; // iterate over the original list
struct node* next;
while (current != NULL) {
next = current->next; // tricky - note the next pointer before we change it
SortedInsert(&result, current);
current = next;
}
*headRef = result;
}
|
|
Write an Append() function that takes two lists, 'a' and 'b', appends 'b' onto the
end of 'a', and then sets 'b' to NULL (since it is now trailing off the end of 'a').
Here is a drawing of a sample call to Append(a, b) with the start state in gray
and the end state in black. At the end of the call, the 'a' list is {1, 2, 3, 4},
and 'b' list is empty.
|
The case where the 'a' list is empty is a special case handled first — in that case
the 'a' head pointer needs to be changed directly. Otherwise we iterate down the
'a' list until we find its last node with the test (current->next != NULL), and
then tack on the 'b' list there. Finally, the original 'b' head is set to NULL.
This code demonstrates extensive use of pointer reference parameters, and the common
problem of needing to locate the last node in a list. (There is also a drawing of
how Append() uses memory below.)
void Append(struct node** aRef, struct node** bRef) {
struct node* current;
if (*aRef == NULL) { // Special case if a is empty
*aRef = *bRef;
}
else { // Otherwise, find the end of a, and append b there
current = *aRef;
while (current->next != NULL) { // find the last node
current = current->next;
}
current->next = *bRef; // hang the b list off the last node
}
*bRef=NULL; // NULL the original b, since it has been appended above
}
Append() Test and Drawing The following AppendTest() code calls Append() to join
two lists. What does memory look like just before the call to Append() exits?
void AppendTest()
{
struct node* a;
struct node* b;
// set a to {1, 2}
// set b to {3, 4}
Append(&a, &b);
}
As an example of how reference parameters work, note how reference parameters in
Append() point back to the head pointers in AppendTest()...
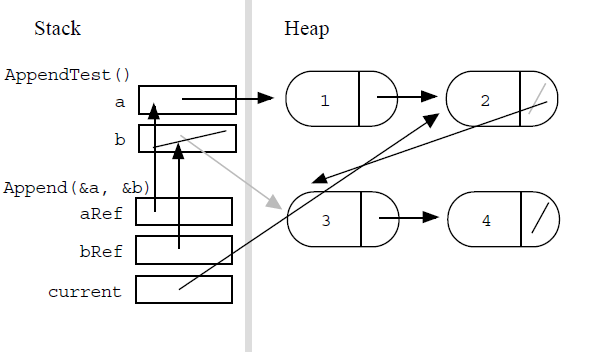
|
|
FrontBackSplit - Given a list, split it into two sublists — one for the front half,
and one for the back half. If the number of elements is odd, the extra element should
go in the front list. So FrontBackSplit() on the list {2, 3, 5, 7, 11} should yield
the two lists {2, 3, 5} and {7, 11}. Getting this right for all the cases is harder
than it looks. You should check your solution against a few cases (length = 2, length
= 3, length=4) to make sure that the list gets split correctly near the short-list
boundary conditions. If it works right for length=4, it probably works right for
length=1000. You will probably need special case code to deal with the (length <2)
cases.
|
Two solutions are presented...
// Uses the "count the nodes" strategy
void FrontBackSplit(struct node* source, struct node** frontRef, struct node** backRef)
{
int len = Length(source);
int i;
struct node* current = source;
if (len < 2) {
*frontRef = source;
*backRef = NULL;
}
else {
int hopCount = (len-1)/2; //(figured these with a few drawings)
for (i = 0; i < hopCount; i++) {
current = current->next;
}
// Now cut at current
*frontRef = source;
*backRef = current->next;
current->next = NULL;
}
}
// Uses the fast/slow pointer strategy
void FrontBackSplit2(struct node* source, struct node** frontRef, struct node** backRef)
{
struct node* fast;
struct node* slow;
if (source==NULL || source->next==NULL) { // length < 2 cases
*frontRef = source;
*backRef = NULL;
}
else {
slow = source;
fast = source->next;
// Advance 'fast' two nodes, and advance 'slow' one node
while (fast != NULL) {
fast = fast->next;
if (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
}
// 'slow' is before the midpoint in the list, so split it in two at that point.
*frontRef = source;
*backRef = slow->next;
slow->next = NULL;
}
}
|
|
Remove Duplicates - Write a RemoveDuplicates() function which takes a list sorted
in increasing order and deletes any duplicate nodes from the list. Ideally, the
list should only be traversed once.
|
Since the list is sorted, we can proceed down the list and compare adjacent nodes.
When adjacent nodes are the same, remove the second one. There's a tricky case where
the node after the next node needs to be noted before the deletion.
// Remove duplicates from a sorted list
void RemoveDuplicates(struct node* head)
{
struct node* current = head;
if (current == NULL) return; // do nothing if the list is empty
// Compare current node with next node
while(current->next!=NULL) {
if (current->data == current->next->data) {
struct node* nextNext = current->next->next;
free(current->next);
current->next = nextNext;
}
else {
current = current->next; // only advance if no deletion
}
}
}
|
|
Move Node - This is a variant on Push(). Instead of creating a new node and pushing
it onto the given list, MoveNode() takes two lists, removes the front node from
the second list and pushes it onto the front of the first. This turns out to be
a handy utility function to have for several later problems. Both Push() and MoveNode()
are designed around the feature that list operations work most naturally at the
head of the list. Here's a simple example of what MoveNode() should do...
|
The MoveNode() code is most similar to the code for Push(). It's short — just changing
a couple pointers — but it's complex. Make a drawing.
void MoveNode(struct node** destRef, struct node** sourceRef)
{
struct node* newNode = *sourceRef; // the front source node
assert(newNode != NULL);
*sourceRef = newNode->next; // Advance the source pointer
newNode->next = *destRef; // Link the old dest off the new node
*destRef = newNode; // Move dest to point to the new node
}
|
|
Alternating Split - Write a function AlternatingSplit() that takes one list and
divides up its nodes to make two smaller lists. The sublists should be made from
alternating elements in the original list. So if the original list is {a, b, a,
b, a}, then one sublist should be {a, a, a} and the other should be {b, b}. You
may want to use MoveNode() as a helper. The elements in the new lists may be in
any order (for some implementations, it turns out to be convenient if they are in
the reverse order from the original list.)
|
The simplest approach iterates over the source list and use MoveNode() to pull nodes
off the source and alternately put them on 'a' and b'. The only strange part is
that the nodes will be in the reverse order that they occurred in the source list.
AlternatingSplit()
void AlternatingSplit(struct node* source, struct node** aRef, struct node** bRef)
{
struct node* a = NULL; // Split the nodes to these 'a' and 'b' lists
struct node* b = NULL;
struct node* current = source;
while (current != NULL) {
MoveNode(&a, ¤t); // Move a node to 'a'
if (current != NULL) {
MoveNode(&b, ¤t); // Move a node to 'b'
}
}
*aRef = a;
*bRef = b;
}
AlternatingSplit() Using Dummy Nodes Here is an alternative approach which builds
the sub-lists in the same order as the source list. The code uses a temporary dummy
header nodes for the 'a' and 'b' lists as they are being built. Each sublist has
a "tail" pointer which points to its current last node — that way new nodes can
be appended to the end of each list easily. The dummy nodes give the tail pointers
something to point to initially. The dummy nodes are efficient in this case because
they are temporary and allocated in the stack. Alternately, the "local references"
technique could be used to get rid of the dummy nodes (see Section 1 for more details).
void AlternatingSplit2(struct node* source, struct node** aRef, struct node** bRef)
{
struct node aDummy;
struct node* aTail = &aDummy; // points to the last node in 'a'
struct node bDummy;
struct node* bTail = &bDummy; // points to the last node in 'b'
struct node* current = source;
aDummy.next = NULL;
bDummy.next = NULL;
while (current != NULL) {
MoveNode(&(aTail->next), ¤t); // add at 'a' tail
aTail = aTail->next; // advance the 'a' tail
if (current != NULL) {
MoveNode(&(bTail->next), ¤t);
bTail = bTail->next;
}
}
*aRef = aDummy.next;
*bRef = bDummy.next;
}
|
|
Suffle Merge - Given two lists, merge their nodes together to make one list, taking
nodes alternately between the two lists. So ShuffleMerge() with {1, 2, 3} and {7,
13, 1} should yield {1, 7, 2, 13, 3, 1}. If either list runs out, all the nodes
should be taken from the other list. The solution depends on being able to move
nodes to the end of a list as discussed in the Section 1 review. You may want to
use MoveNode() as a helper. Overall, many techniques are possible: dummy node, local
reference, or recursion. Using this function and FrontBackSplit(), you could simulate
the shuffling of cards.
|
There are four separate solutions included. See Section 1 for information on the
various dummy node and reference techniques.
SuffleMerge() — Dummy Node Not Using MoveNode()
struct node* ShuffleMerge(struct node* a, struct node* b)
{
struct node dummy;
struct node* tail = &dummy;
dummy.next = NULL;
while (1) {
if (a==NULL) { // empty list cases
tail->next = b;
break;
}
else if (b==NULL) {
tail->next = a;
break;
}
else { // common case: move two nodes to tail
tail->next = a;
tail = a;
a = a->next;
tail->next = b;
tail = b;
b = b->next;
}
}
return(dummy.next);
}
SuffleMerge() — Dummy Node Using MoveNode() Basically the same as above, but use MoveNode().
struct node* ShuffleMerge(struct node* a, struct node* b)
{
struct node dummy;
struct node* tail = &dummy;
dummy.next = NULL;
while (1) {
if (a==NULL) {
tail->next = b;
break;
}
else if (b==NULL) {
tail->next = a;
break;
}
else {
MoveNode(&(tail->next), &a);
tail = tail->next;
MoveNode(&(tail->next), &b);
tail = tail->next;
}
}
return(dummy.next);
}
SuffleMerge() — Local References Uses a local reference to get rid of the dummy nodes entirely.
struct node* ShuffleMerge(struct node* a, struct node* b)
{
struct node* result = NULL;
struct node** lastPtrRef = &result;
while (1) {
if (a == NULL) {
*lastPtrRef = b;
break;
}
else if (b == NULL) {
*lastPtrRef = a;
break;
}
else {
MoveNode(lastPtrRef, &a);
lastPtrRef = &((*lastPtrRef)->next);
MoveNode(lastPtrRef, &b);
lastPtrRef = &((*lastPtrRef)->next);
}
}
return(result);
}
SuffleMerge() — Recursive
The recursive solution is the most compact of all, but is probably not appropriate for
production code since it uses stack space proportionate to the lengths of the lists.
struct node* ShuffleMerge(struct node* a, struct node* b)
{
struct node* result;
struct node* recur;
if (a == NULL) return(b); // see if either list is empty
else if (b == NULL) return(a);
else {
// it turns out to be convenient to do the recursive call first --
// otherwise a->next and b->next need temporary storage.
recur = ShuffleMerge(a->next, b->next);
result = a; // one node from a
a->next = b; // one from b
b->next = recur; // then the rest
return(result);
}
}
|
|
Sorted Merge - Write a SortedMerge() function that takes two lists, each of which
is sorted in increasing order, and merges the two together into one list which is
in increasing order. SortedMerge() should return the new list. The new list should
be made by splicing together the nodes of the first two lists (use MoveNode()).
Ideally, Merge() should only make one pass through each list. Merge() is tricky
to get right — it may be solved iteratively or recursively. There are many cases
to deal with: either 'a' or 'b' may be empty, during processing either 'a' or 'b'
may run out first, and finally there's the problem of starting the result list empty,
and building it up while going through 'a' and 'b'.
|
SortedMerge() Using Dummy Nodes
The strategy here uses a temporary dummy node as the start of the result list. The pointer
tail always points to the last node in the result list, so appending new nodes is easy.
The dummy node gives tail something to point to initially when the result list is empty.
This dummy node is efficient, since it is only temporary, and it is allocated in the stack.
The loop proceeds, removing one node from either 'a' or 'b', and adding it to tail. When
we are done, the result is in dummy.next.
struct node* SortedMerge(struct node* a, struct node* b)
{
struct node dummy; // a dummy first node to hang the result on
struct node* tail = &dummy; // Points to the last result node --
// so tail->next is the place to add
// new nodes to the result.
dummy.next = NULL;
while (1) {
if (a == NULL) { // if either list runs out, use the other list
tail->next = b;
break;
}
else if (b == NULL) {
tail->next = a;
break;
}
if (a->data <= b->data) {
MoveNode(&(tail->next), &a);
}
else {
MoveNode(&(tail->next), &b);
}
tail = tail->next;
}
return(dummy.next);
}
SortedMerge() Using Local References
This solution is structurally very similar to the above, but it avoids using a dummy node.
Instead, it maintains a struct node** pointer, lastPtrRef, that always points to the last
pointer of the result list. This solves the same case that the dummy node did — dealing
with the result list when it is empty. If you are trying to build up a list at its tail, either the
dummy node or the struct node** "reference" strategy can be used (see Section 1 for
details).
struct node* SortedMerge2(struct node* a, struct node* b)
{
struct node* result = NULL;
struct node** lastPtrRef = &result; // point to the last result pointer
while (1) {
if (a==NULL) {
*lastPtrRef = b;
break;
}
else if (b==NULL) {
*lastPtrRef = a;
break;
}
if (a->data <= b->data) {
MoveNode(lastPtrRef, &a);
}
else {
MoveNode(lastPtrRef, &b);
}
lastPtrRef = &((*lastPtrRef)->next); // tricky: advance to point to
// the next ".next" field
}
return(result);
}
SortedMerge() Using Recursion
Merge() is one of those nice recursive problems where the recursive solution code is
much cleaner than the iterative code. You probably wouldn't want to use the recursive
version for production code however, because it will use stack space which is
proportional to the length of the lists.
struct node* SortedMerge3(struct node* a, struct node* b)
{
struct node* result = NULL;
// Base cases
if (a==NULL) return(b);
else if (b==NULL) return(a);
// Pick either a or b, and recur
if (a->data <= b->data) {
result = a;
result->next = SortedMerge3(a->next, b);
}
else {
result = b;
result->next = SortedMerge3(a, b->next);
}
return(result);
}
|
|
Merge Sort - (This problem requires recursion) Given FrontBackSplit() and SortedMerge(),
it's pretty easy to write a classic recursive MergeSort(): split the list into two
smaller lists, recursively sort those lists, and finally merge the two sorted lists
together into a single sorted list. Ironically, this problem is easier than either
FrontBackSplit() or SortedMerge().
|
The MergeSort strategy is: split into sublists, sort the sublists recursively, merge
the two sorted lists together to form the answer.
void MergeSort(struct node** headRef)
{
struct node* head = *headRef;
struct node* a;
struct node* b;
// Base case -- length 0 or 1
if ((head == NULL) || (head->next == NULL)) {
return;
}
FrontBackSplit(head, &a, &b); // Split head into 'a' and 'b' sublists
// We could just as well use AlternatingSplit()
MergeSort(&a); // Recursively sort the sublists
MergeSort(&b);
*headRef = SortedMerge(a, b); // answer = merge the two sorted lists together
}
(Extra for experts) Using recursive stack space proportional to the length of a
list is not recommended. However, the recursion in this case is ok — it uses stack
space which is proportional to the log of the length of the list. For a 1000 node
list, the recursion will only go about 10 deep. For a 2000 node list, it will go
11 deep. If you think about it, you can see that doubling the size of the list only
increases the depth by 1.
|
|
Sorted Intersect - Given two lists sorted in increasing order, create and return
a new list representing the intersection of the two lists. The new list should be
made with its own memory — the original lists should not be changed. In other words,
this should be Push() list building, not MoveNode(). Ideally, each list should only
be traversed once. This problem along with Union() and Difference() form a family
of clever algorithms that exploit the constraint that the lists are sorted to find
common nodes efficiently.
|
The strategy is to advance up both lists and build the result list as we go. When
the current point in both lists are the same, add a node to the result. Otherwise,
advance whichever list is smaller. By exploiting the fact that both lists are sorted,
we only traverse each list once. To build up the result list, both the dummy node
and local reference strategy solutions are shown... // This solution uses the temporary
dummy to build up the result list
struct node* SortedIntersect(struct node* a, struct node* b)
{
struct node dummy;
struct node* tail = &dummy;
dummy.next = NULL;
// Once one or the other list runs out -- we're done
while (a!=NULL && b!=NULL) {
if (a->data == b->data) {
Push((&tail->next), a->data);
tail = tail->next;
a = a->next;
b = b->next;
}
else if (a->data < b->data) { // advance the smaller list
a = a->next;
}
else {
b = b->next;
}
}
return(dummy.next);
}
// This solution uses the local reference
struct node* SortedIntersect2(struct node* a, struct node* b)
{
struct node* result = NULL;
struct node** lastPtrRef = &result;
// Advance comparing the first nodes in both lists.
// When one or the other list runs out, we're done.
while (a!=NULL && b!=NULL) {
if (a->data == b->data) { // found a node for the intersection
Push(lastPtrRef, a->data);
lastPtrRef = &((*lastPtrRef)->next);
a = a->next;
b = b->next;
}
else if (a->data < b->data) { // advance the smaller list
a = a->next;
}
else {
b = b->next;
}
}
return(result);
}
|
|
Reverse - Write an iterative Reverse() function that reverses a list by rearranging
all the .next pointers and the head pointer. Ideally, Reverse() should only need
to make one pass of the list. The iterative solution is moderately complex. It's
not so difficult that it needs to be this late in the document, but it goes here
so it can be next to #18 Recursive Reverse which is quite tricky.
|
This first solution uses the "Push" strategy with the pointer re-arrangement hand
coded inside the loop. There's a slight trickyness in that it needs to save the
value of the "current->next" pointer at the top of the loop since the body of the
loop overwrites that pointer.
/*
Iterative list reverse.
Iterate through the list left-right.
Move/insert each node to the front of the result list --
like a Push of the node.
*/
static void Reverse(struct node** headRef)
{
struct node* result = NULL;
struct node* current = *headRef;
struct node* next;
while (current != NULL) {
next = current->next; // tricky: note the next node
current->next = result; // move the node onto the result
result = current;
current = next;
}
*headRef = result;
}
Here's the variation on the above that uses MoveNode() to do the work...
static void Reverse2(struct node** headRef)
{
struct node* result = NULL;
struct node* current = *headRef;
while (current != NULL) {
MoveNode(&result, ¤t);
}
*headRef = result;
}
Finally, here's the back-middle-front strategy...
// Reverses the given linked list by changing its .next pointers and
// its head pointer. Takes a pointer (reference) to the head pointer.
void Reverse(struct node** headRef)
{
if (*headRef != NULL) { // special case: skip the empty list
/*
Plan for this loop: move three pointers: front, middle, back
down the list in order. Middle is the main pointer running
down the list. Front leads it and Back trails it.
For each step, reverse the middle pointer and then advance all
three to get the next node.
*/
struct node* middle = *headRef; // the main pointer
struct node* front = middle->next; // the two other pointers (NULL ok)
struct node* back = NULL;
while (1) {
middle->next = back; // fix the middle node
if (front == NULL) break; // test if done
back = middle; // advance the three pointers
middle = front;
front = front->next;
}
*headRef = middle; // fix the head pointer to point to the new front
}
}
|
|
Recursive Reverse - There is a short and efficient recursive solution to this problem.
As before, the code should only make a single pass over the list. Doing it with
multiple passes is easier but very slow, so here we insist on doing it in one pass..
Solving this problem requires a real understanding of pointer code and recursion.
|
Probably the hardest part is accepting the concept that the RecursiveReverse(&rest)
does in fact reverse the rest. Then then there's a trick to getting the one front
node all the way to the end of the list. Make a drwaing to see how the trick works.
void RecursiveReverse(struct node** headRef)
{
struct node* first;
struct node* rest;
if (*headRef == NULL) return; // empty list base case
first = *headRef; // suppose first = {1, 2, 3}
rest = first->next; // rest = {2, 3}
if (rest == NULL) return; // empty rest base case
RecursiveReverse(&rest); // Recursively reverse the smaller {2, 3} case
// after: rest = {3, 2}
first->next->next = first; // put the first elem on the end of the list
first->next = NULL; // (tricky step -- make a drawing)
*headRef = rest; // fix the head pointer
}
The inefficient soluition is to reverse the last n-1 elements of the list, and then
iterate all the way down to the new tail and put the old head node there. That solution
is very slow compared to the above which gets the head node in the right place without
extra iteration.
|
|
Basic utility functions.
|
Length()
// Return the number of nodes in a list
int Length(struct node* head)
{
int count = 0;
struct node* current = head;
while (current != NULL) {
count++;
current=current->next;
}
return(count);
}
Push()
// Given a reference (pointer to pointer) to the head
// of a list and an int, push a new node on the front of the list.
// Creates a new node with the int, links the list off the .next of the
// new node, and finally changes the head to point to the new node.
void Push(struct node** headRef, int newData)
{
struct node* newNode =
(struct node*) malloc(sizeof(struct node)); // allocate node
newNode->data = newData; // put in the data
newNode->next = (*headRef); // link the old list off the new node
(*headRef) = newNode; // move the head to point to the new node
}
BuildOneTwoThree()
// Build and return the list {1, 2, 3}
struct node* BuildOneTwoThree()
{
struct node* head = NULL; // Start with the empty list
Push(&head, 3); // Use Push() to add all the data
Push(&head, 2);
Push(&head, 1);
return(head);
}
|